[ CAPÍTULO 3 ]
Caos
Aprendendo a abandonar o controle
Na filosofia existe um princípio denominado determinismo que defende que todos os eventos que já aconteceram e irão suceder são resultados de estados e ações passadas. De certa forma, o que você realizou nos capítulos anteriores se encaixa nesse pensamento. Você aprendeu a posicionar, com precisão cirúrgica, figuras geométricas, assim como definir repetições e condicionais cujas consequências eram completamente conhecidas antes mesmo da execução do programa. Apesar de isso ser um feito incrível, sempre que você pressionar o botão de executar o resultado será o mesmo. Em pouco tempo o previsível se torna desinteressante.
No espectro oposto desse raciocínio está o caos, em que é impossível prever qualquer consequência, pois elas são independentes e descorrelacionadas de todas e quaisquer ações. Aqui reina o imprevisível e a completa ausência de lógica. Um pandemônio que termina em indiferença.
No centro dessa dualidade nasce o núcleo do que faz o mundo interessante. É o familiar, mas cheio de surpresas, o caos controlado. Na natureza é isso que faz as árvores terem forma de árvores, e nunca serem absolutamente iguais umas às outras. O mesmo vale para as nuvens, para os animais e as pessoas. Sucintamente, a forma é mantida, o conteúdo não. Neste capítulo você entenderá como aplicar esse conceitos para transformar a arte computacional na intrigante arte gerativa.
A arte gerativa está intrinsecamente ligada à falta de uniformidade e à capacidade de criar infinitas figuras e padrões usando microvariações presentes durante a execução do código. Uma maneira de forçar essas variações é parametrizando elementos do código tais como variáveis, condicionais e repetições e, de alguma forma, alterá-los. Existem dois grandes fatores que contribuem profundamente para uma boa arte gerativa:
São eles o "o que" deve ser parametrizado no código e o "como" deve ser parametrizado.
O o que deve ser parametrizado é usualmente definido na etapa de concepção da arte para criar uma forma, molde ou configuração distinguível na escala macro. No exemplo citado da árvore, consiste em saber que ela sempre possuirá um tronco, galhos, folhas e flores, mas não é estabelecido o número, tamanho ou cores desses elementos.
O como deve ser parametrizado é normalmente definido na etapa de simulação para criar uma execução marcante na escala micro, evidenciada nos detalhes. Para a árvore, isso implicaria em definir que, quando ela tem entre 6 e 10 metros de altura, copa ampla de 3 a 6 metros e flores de 5 a 8 cm com diversos tons de amarelo ela possuirá uma estética deslumbrante (3.1). Na computação artística é ideal experimentar com esses valores durante ou após a execução do código, pois assim você pode ajustá-los sucessivamente até obter um resultado que goste.

Um modo de alterar o valor dos elementos parametrizados é utilizando a aleatoriedade para gerar números diferentes toda vez que o programa for executado. No entanto humanos não são muito bons nessa tarefa[1] [2] e diversas vezes tendem a se repetir, produzindo resultados similares. Por outro lado, máquinas são excelentes em gerar números imprevisíveis[3] e por isso você usará o computador para automatizar as variações desejadas.
O primeiro método para obter números aleatórios que você irá estudar é através da função random() , que gera um número qualquer, baseado em uma distribuição uniforme[4] , entre os argumentos fornecidos. Por exemplo:
- random(5,10): Gera um número aleatório entre 5 e 10.
- random(0,10) ou random(10): Gera um número aleatório entre 0 e 10.
- random(height): Gera um número aleatório entre 0 e a altura da janela de exibição.
Note que a função random(10) é numericamente igual a função 10*random(1) uma vez que random(1) gera um número entre 0 e 1 que, multiplicado por 10, resulta em número entre 0 e 10. Em alguns casos é mais interessante utilizar este segundo tipo de notação, uma vez que remete a funções de distribuição probabilística na matemática. Algumas funções equivalentes são:
- random(30) ↔ 30*random(1).
- random(5,20) ↔ (5 + random(15)) ↔ (5 + 15*random(1)).
- Genericamente, random(min,max) é escrito como (min + (max-min)*random(1)).
Se você quiser visualizar os números gerados pode escrever um código para exibí-los no console:
Código 3.1 -
for(int i = 0; i < 100; i++) {
println(random(1000));
}
Transferindo para a tabela 3.1 teríamos:
| 645.9 | 594.3 | 071.9 | 647.0 | 743.5 | 394.5 | 357.1 | 260.1 | 699.1 | 229.4 |
| 422.8 | 438.6 | 764.0 | 918.5 | 814.5 | 317.7 | 362.5 | 355.9 | 966.2 | 567.8 |
| 231.0 | 066.8 | 399.8 | 315.1 | 800.0 | 474.6 | 687.1 | 242.1 | 317.1 | 160.6 |
| 521.6 | 056.0 | 513.2 | 530.1 | 742.6 | 925.0 | 145.2 | 536.8 | 159.2 | 033.1 |
| 212.3 | 286.7 | 553.5 | 830.8 | 682.9 | 148.8 | 394.0 | 113.6 | 052.1 | 302.0 |
| 004.5 | 757.0 | 278.3 | 681.7 | 192.4 | 810.1 | 636.1 | 947.7 | 499.8 | 998.8 |
| 740.6 | 144.9 | 194.2 | 320.8 | 607.3 | 085.8 | 113.0 | 917.6 | 741.3 | 460.2 |
| 329.6 | 369.8 | 222.0 | 211.5 | 965.7 | 844.2 | 839.0 | 651.5 | 060.8 | 501.7 |
| 032.2 | 096.8 | 268.4 | 394.1 | 617.8 | 859.1 | 924.7 | 894.5 | 691.6 | 229.5 |
| 169.3 | 937.7 | 267.0 | 552.2 | 839.3 | 941.3 | 943.2 | 632.3 | 667.4 | 805.5 |
Em forma de texto, como a tabela 3.1, é difícil ver o quão significativo são ou não esses números. Felizmente o Processing é uma linguagem voltada para visualizações e é possível ver uma representação gráfica da função random(). Inicialmente vamos desenvolver um programa que, para cada pixel do eixo x (largura) dessa janela, seja gerado um ponto y aleatório e traçado uma reta ligando o ponto anterior gerado ao atual. Esta é uma análise unidimensional de uma distribuição aleatória, já que os pontos do eixo y são a única incógnita no ato da execução do programa. O código abaixo mostra como realizar isso e o resultado pode ser visto na figura 3.2.
Código 3.2 - Distribuição aleatória -
size(400,200);
background(255);
float xAnterior = 0;
float yAnterior = height*random(1);
for(int i = 1; i < width; i++) {
float y = height*random(1);
line(xAnterior,yAnterior,i,y);
yAnterior = y;
xAnterior = i;
}
}
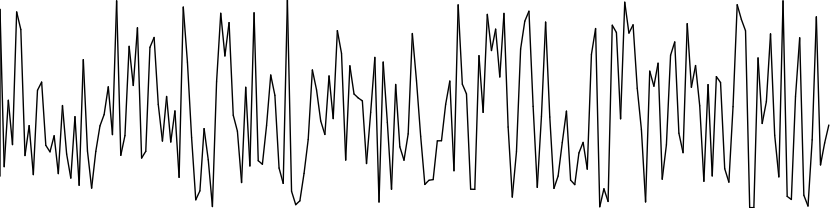
Imediatamente, o que você pode perceber é uma distribuição muito errática, uma curva abundante em picos e vales. Na prática, isso significa que cada vez que você chama a função random() ela retorna um número que não tem nenhuma relação com qualquer outro que foi ou será gerado por ela. Consequentemente nada impede que ocorram diferenças gigantescas entre números de iterações sequenciais. Por exemplo, se você chamar a função random(1000) duas vezes seguidas, na primeira pode obter 0.00 e na segunda 999.99, obtendo a maior amplitude possível do intervalo.
Números puramente aleatórios podem ser usados de diversas formas para influenciar o comportamento de seu programa. Se usados para movimentar figuras, podem implicar em variações bruscas e descontínuas ou grandes alterações nas direções de objetos. Ao serem aplicados para colorir figuras, as cores raramente irão manter um tom harmônico, que pode ser bom ou ruim, depende do efeito que você deseja causar. Em geral, usar números fornecidos pela função random(), sem nenhum tipo de ajuste, pode resultar em uma impressão de sintético e não naturalidade, seja do movimento ou variação. Tal fato pode ser exemplificado pelo código abaixo, que dispõe figuras aleatóriamente na tela e as colore com a função random(). Veja a imagem gerada na figura 3.3.
Código 3.3 - Cores aleatórias -
size(400,150);
noStroke();
for(int i = 0; i < 500; i++) {
// Posição aleatória na janela:
float x = random(width);
float y = random(height);
// Cor aleatória:
float r = random(255);
float g = random(255);
float b = random(255);
fill(r,g,b);
rect(x,y,30,30);
}
}

A aleatoriedade pura, introduzida na seção passada, tem um papel importante ao gerar números descorrelacionados. No entanto ela desaponta ao ser muito brusca e, ironicamente, muito imprevisível, podendo criar visuais mecânicos e frios. Foi devido a esse fenômeno que em 1983 o Dr. Ken Perlin, um professor de ciências da computação, inventou o ruído Perlin[5] , um algoritmo capaz de gerar uma sequência naturalmente ordenada de números pseudo-aleatórios. Calma, essa frase complicada significa apenas que o Dr. Perlin conseguiu criar um algoritmo que gera números aleatórios com uma distribuição suave, natural e, ultimamente, orgânica. A linguagem Processing possuí esse algoritmo[6] convenientemente programado através da função noise().
A chamada da função noise() não é tão direta quanto a random() e existem alguns detalhes que podem ser melhor consultados em sua referência. Os mais importantes para o seu funcionamento correto são:
- A função noise() sempre devolve um número entre 0 e 1.
- A função deve receber argumentos de entrada que estejam constantemente variando. Quanto menores as variações dos parâmetros entre as chamadas da função, menores serão as diferenças entre os números gerados. Um parâmetro fixo sempre fornecerá o mesmo valor de ruído.
A forma mais básica de sua chamada é:
Código 3.4 -
O truque para entender essas peculiaridades está na maneira de enxergar essa função. Você deve imaginar a função noise() como um "observador" de uma curva aleatória. Essa curva é completamente construída no início da execução do seu programa e, quando você passa um argumento para a função noise(), você simplesmente realiza uma consulta a um ponto dessa curva. As figuras 3.4 e 3.5 exemplificam essa ideia.
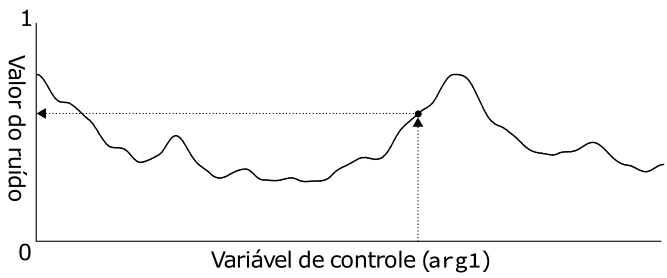
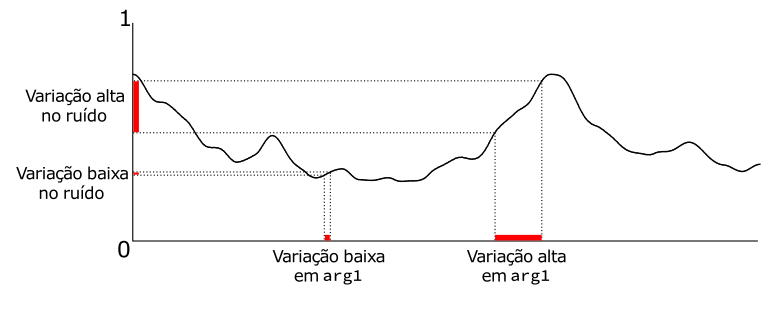
Essa interpretação também explica a necessidade dos parâmetros dessa função estarem sempre variando, caso contrário você estaria consultando sempre o mesmo "ponto" da curva e recebendo um valor estático.
Para fazer a comparação com a função random(), iremos traçar a curva da figura 3.2 usando a função noise(). Será necessário criar uma variável auxiliar e incrementá-la antes de cada invocação da função para que a mesma retorne valores diferentes. Adaptando o código 3.2 você pode escrever:
Código 3.5 - Distribuição ruidosa -
size(400,200);
background(255);
float ruido = 0;
float amplitudeRuido = 1;
float xAnterior = 0;
float yAnterior = height*noise(ruido);
for(int i = 1; i < width; i++) {
float y = height*noise(ruido);
line(xAnterior,yAnterior,i,y);
yAnterior = y;
xAnterior = i;
ruido += amplitudeRuido;
}
}
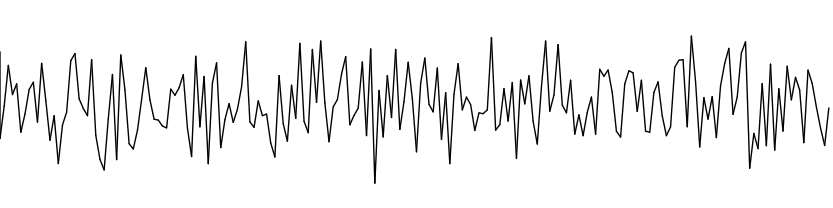
Uma análise rápida da distribuição resultante, figura 3.6, nos leva à conclusão de que a função noise() é ineficaz dado que comportamento da curva não mudou. A amplitude entre amostras adjacentes continua extremamente alta, sendo indesejado para criar sequências orgânicas. No entanto devemos ter cuidado com inferências precipitadas e, em caso de dúvidas, retornar à página de ajuda da linguagem.
Lembre-se que a função noise() terá um comportamento que dependerá diretamente da variação em seus argumentos a cada vez que ela for chamada. Se o passo (ou diferença) entre o argumento anterior e o próximo for muito alto você terá grandes amplitudes, e se for muito baixo, terá uma saída quase que constante. O segredo é experimentar com diversos valores até encontrar um se adapte com o tipo de resposta que você deseja obter. A referência do Processing sugere que variações contidas no intervalo de 0.005 a 0.03 entre chamadas da função noise() atendem a grande parte das aplicações. No código 3.5 o passo foi parametrizado pela variável amplitudeRuido. Na figura 3.7 é mostrado exatamente o mesmo programa com valores diferentes para essa variável.

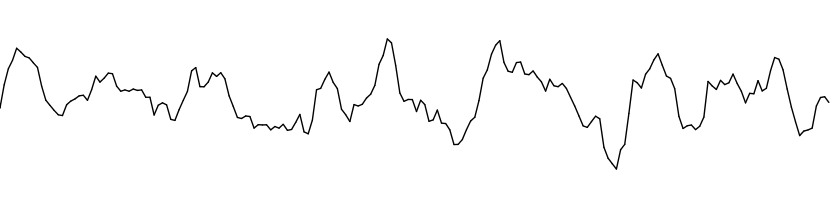


Observe como o comportamento da curva foi alterado significativamente de acordo com o argumento da função. Perceba também uma amenização na turbulência das curvas em comparação com as da função random(). Quando esses valores forem usados para direcionar um movimento ou alterar uma cor, a ilusão criada será de uma variação orgânica e natural. O código abaixo é uma adaptação do 3.3, e cria cores com transições suaves, quase que contínuas, exibidas na figura 3.12.
Código 3.6 - Cores ruidosas -
size(400,150);
noStroke();
// Variáveis que controlam o ruído das cores:
float nr = 0, ng = 100, nb = 200;
for(int i = 0; i < 500; i++) {
float x = random(width);
float y = random(height);
float r = 255*noise(nr);
float g = 255*noise(ng);
float b = 255*noise(nb);
fill(r,g,b);
rect(x,y,30,30);
// Incremento das variáveis para produzir ruídos distintos:
nr += 0.01;
ng += 0.01;
nb += 0.01;
}
}

Nas duas primeiras seções deste capítulo você observou como as funções random() e noise() são peças fundamentais para incluir o caos em seus programas. Nos dois códigos, 3.2 e 3.5, foram geradas visualizações bidimensionais de uma variação unidimensional, referente à análise da diferença entre um número aleatório e o seu sucessor. O objetivo de tais figuras foi facilitar a comparação do aspecto brusco ou suave proveniente dessas funções.
Uma segunda maneira de criar um padrão visual e simultaneamente comparar as funções random() e noise() é através de uma distribuição e figura verdadeiramente bidimensional, formada por um plano de duas dimensões: a janela de saída. Definindo uma janela do tipo size(300,150), existirão um total de 45000 pixels que podem ser coloridos conforme nossa vontade. Você pode automatizar a tarefa de referenciar os pixels sequencialmente se criar duas estruturas de repetição aninhadas (seção 2.5.2) projetadas para percorrer a largura e a altura da tela. Assim, para cada índice gerado pelas repetições, você pode colorir o respectivo pixel usando a escala de cinza cuja cor será fornecida tanto pela função random() quanto pela noise(). O aninhamento de repetições para o primeiro caso pode ser escrito como:
Código 3.7 -
size(300,150);
background(255);
// Varre todos os pixels da janela e os preenche com uma cor aleatória:
for(int i = 0; i < width; i++) {
for(int j = 0; j < height; j++) {
stroke(color(random(255)));
point(i,j);
}
}
}
A função noise() requer sua versão correspondente de dois argumentos, com elementos declarados e incrementados individualmente. Também deve-se atentar ao cuidado de "reiniciar" uma das dimensões do ruído quando for dado um passo na repetição mais externa. O preenchimento da janela é feito a seguir:
Código 3.8 -
size(300,150);
background(255);
float amplitudeRuido = 0.05;
float ruidoX = 0;
float ruidoY = 100;
// Varre todos os pixels da janela e os preenche com uma cor ruidosa:
for(int i = 0; i < width; i++) {
for(int j = 0; j < height; j++) {
ruidoY += amplitudeRuido;
stroke(color(255*noise(ruidoX,ruidoY)));
point(i,j);
}
// Reinicia a variável ruidoY para seu valor inicial, e incrementa ruidoX:
ruidoY = 100;
ruidoX += amplitudeRuido;
}
}
A figura 3.13 mostra o resultado para a função random() e a figura 3.14 para a função noise(). Vamos analisar as imagens de acordo com o que foi explicado nas seções anteriores. A imagem produzida pela função random() se assimila a uma estática de televisão. Isso era esperado uma vez que essa função gera elementos aleatórios independentes um do outro, sendo muito provável que a amplitude entre o máximo e o mínimo de uma cor seja alta, produzindo pixels claros (cores próximas a 255) e escuros (cores próximas a 0) lado a lado, correspondendo ao efeito visual de estática. Por sua vez a função noise() também gera valores aleatórios, no entanto eles não variam muito entre si (dependendo do passo) gerando uma figura muito mais suave, algo parecido com uma neblina, nuvem, mármore ou floresta. Essa classe de ruído permite criar texturas gerativas e foi justamente por esse tipo de efeito visual que o Dr. Perlin recebeu o Academy Award for Technical Achievement em efeitos especiais em 1997, uma espécie de Oscar técnico da indústria cinematográfica.



Por exemplo, se você jogar uma moeda para cima e aguardar ela cair só existem duas opções[7], cara ou coroa, portanto o universo de possibilidades é dois. Quanto as probabilidades, temos 50% (ou metade, 1/2) de chance da "cara" estar voltada para cima e 50% de chance da "coroa" estar voltada para cima. Mentalize um segundo cenário em você joga um dado de seis lados, ele sempre cairá em uma das seis faces, ou seja, existe 16.667% (ou 1/6) de chance dele cair no número 1, ou no 2 e assim por diante. E qual a chance de um número ser menor que 3? Bem, o dado possuí 6 lados (todas as possibilidades), e dois desses números (1 e 2) são estritamente menores que três. Usando a definição de probabilidade, a chance é de 2/6, ou 0.333... que equivale a 33.3%.
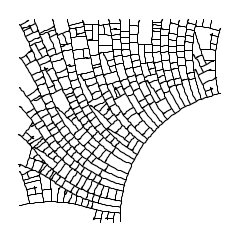
Na arte computacional a probabilidade tem um papel semelhante ao da aleatoriedade: adicionar o elemento da surpresa, mutação e variedade. Em um exemplo concreto, suponha que você desenvolva um algoritmo que crie um ramo central que, aleatóriamente, se derive em ramos secundários e terciários e assim sucessivamente. O que ocorreria se a probabilidade de derivar esses ramos fosse alterada? A figura seria diferente? Em 3.19 está mostrado, visualmente, a resposta dessa pergunta através de um algoritmo inspirado na venação foliar[8]. As diferenças são claramente explícitas mesmo estando vinculadas a poucos coeficientes que controlam as chances de ocorrerem ramificações.
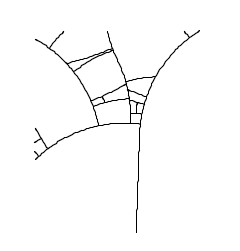
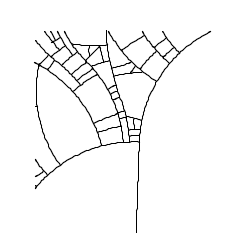
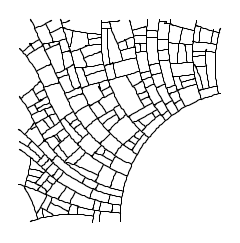
No Processing a maneira mais fácil de se criar uma verificação de probabilidade é através de um condicional usando a função random(). As probabilidades podem ser balanceadas ou não, e isso costuma ser usado para priorizar um evento em relação a outro. O código abaixo mostra a implementação de uma probabilidade qualquer no Processing:
Código 3.9 -
if(random(1) < probabilidade) {
// O código aqui tem 80% de chance de ser executado.
}
else {
// O código aqui tem 20% de chance de ser executado.
}
O ponto chave da probabilidade está na expressão:
Código 3.1 -
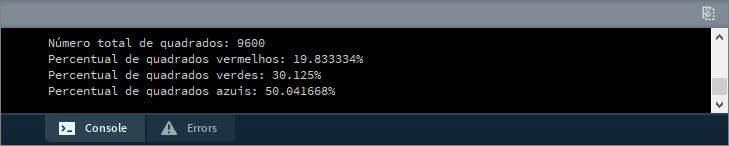
A função random(1) fornece uma distribuição uniforme entre zero e um, logo a chance de gerar qualquer número menor que 0.8 é de 80% uma vez que todo número de 0.0 até 0.7999 é considerado menor que 0.8. Este caso é similar ao exemplo relativo ao jogar do dado do início deste capítulo. Se você quiser adicionar múltiplos testes envolvendo probabilidades também é possível, mas terá de usar o mesmo número gerado para todos os testes. Neste caso os condicionais deverão ser feitos da menor probabilidade para a maior, além de estarem contidos dentro de estruturas else. Isto é ilustrado no código a seguir, que preenche a tela, figura 3.24, com cores baseadas em diferentes probabilidades. Em seguida, para confirmar nosso algoritmo, foi escrito no console, 3.25, o percentual de quadrados de cada cor em relação ao número total.
Código 3.10 -
int vermelho = 0, verde = 0, azul = 0;
void setup() {
size(800,300);
background(255);
noStroke();
for(int i = 0; i < width/5; i++) {
for(int j = 0; j < height/5; j++) {
// Número qualquer entre 0 e 1
float prob = random(1);
if(prob < 0.2) { // 20% de chance do quadrado ser pintado de vermelho.
fill(255,0,0);
vermelho++;
}
else {
if(prob < 0.5) { // 30% de chance do quadrado ser pintado de verde.
fill(0,255,0);
verde++;
}
else { // 50% de chance do quadrado ser pintado de azul.
fill(0,0,255);
azul++;
}
}
rect(i*5,j*5,5,5);
}
}
int total = vermelho+verde+azul;
println("Número total de quadrados:", total);
println("Percentual de quadrados vermelhos:", 100.0*vermelho/total, "%");
println("Percentual de quadrados verdes:", 100.0*verde/total, "%");
println("Percentual de quadrados azuis:", 100.0*azul/total, "%");
}

No caso específico de probabilidades não é vantajoso usar a função noise() dada que ela não fornece números verdadeiramente descorrelacionados e introduziria um viés na possibilidade de um evento ocorrer. Existem outros tipos de distribuições probabilísticas além da uniforme que você acabou de aprender, mas no final todas têm o objetivo de diminuir a monotonia através da manipulação de ocorrências.
Neste capítulo foi explicado como utilizar o Processing para gerar números aleatórios, tanto independentes quanto correlacionados. Quando usados para alterar o valor de variáveis parametrizadas no código elas originam uma variedade infinita de padrões a cada execução do seu programa. Brevemente, você aprendeu sobre:
- Função random(): Responsável por devolver números aleatórios totalmente descorrelacionados dos números gerados anteriormente. Pode ser usado para criar variações e efeitos bruscos ou repentinos.
- Função noise(): Permite gerar números aleatórios baseados em uma variação numérica. Quanto maior essa variação, maior a semelhança dessa função com a aleatoriedade pura. Quanto menor essa variação, menor a amplitude entre amostras, gerando distribuições suaves e naturais.
- Probabilidades: Importante para direcionar e moldar o fluxo ou característica do programa. Enfatiza elementos que devem ser repetidos com mais frequência e introduz eventos ocasionais capazes de impactar significativamente no resultado final da obra.
O principal ponto desta seção é que o caos, na arte gerativa, deve ser moldado e direcionado até o ponto que você deseje que ele atue. Uma vez que esse ponto é atingido você deve aceitá-lo e deixar que ele se expanda através de uma dança anárquica que florescerá em imagens, padrões ou figuras verdadeiramente únicas e belas.
No próximo capítulo você descobrirá como o oposto do que você acabou de estudar também pode ser surpreendentemente cativante. A matemática, personificação das leis que regem o universo, está muitas vezes oculta sobre mantos densos de fórmulas, letras e números, mas uma vez desvelada você compreenderá porque ela sempre fascinou a humanidade.
[1] Wagenaar, W. A. (1972). "Generation of random sequences by human subjects: a critical survey of the literature". Psychological Bulletin 77: pags.65-72.
[2] Brugger, P. (1997). "Variables that influence the generation of random sequences: An update". Perceptual and Motor Skills 84(2): pags.627-661.
[3] Na verdade, um computador não consegue gerar números verdadeiramente aleatórios e sim pseudo-aleatórios. Ênfase no pseudo, pois eles são gerados de acordo com parâmetros do computador como clock, ou através de algoritmos como o Gerador Congruente Linear. O problema da pseudo-aleatoriedade é que uma vez descoberto como os números são gerados eles se tornam determinísticos. Mas não se preocupe, isso é muito mais significativo para a área de criptografia do que para a arte computacional.
[4] Uma distribuição uniforme, ou retangular, é aquela contida entre um máximo e um mínimo de tal forma que a chance de qualquer número ser escolhido dentro dela é a mesma.
[5] Do inglês, Perlin noise.
[6] A versão do Processing é uma simplificação do verdadeiro ruído Perlin.
[7] É muito improvável da moeda cair exatamente "em pé", por isso esse evento foi desconsiderado.
[8] Algoritmo desenvolvido com base no artigo Reunions A. et al (2005). Modeling and visualization of leaf venation patterns. ACM Transactions on Graphics 24(3): pags. 702-711

