[ CAPÍTULO 6 ]
Fractais
Catástase computacional
Em 1989 o pai da geometria fractal, o matemático Benoit B. Mandelbrot, publicou um artigo intitulado Geometria Fractal: o que é, e o que ela faz?[1] em que a definiu em um pequeno parágrafo:
"Geometria fractal é um meio termo geométrico trabalhável entre a excessiva ordem geométrica Euclidiana e o caos geométrico da matemática geral. É baseado em uma forma de simetria que foi préviamente subutilizada, chamada de invariância na presença de contração e dilatação. A geometria fractal é convenientemente vista como uma linguagem que prova seu valor pelos seus usos. É usada na arte e na matemática pura, sem aplicações "práticas", podendo ser dita como sendo poética."
Em um contexto puramente técnico, pode parecer estranho que palavras como "arte" e "poética" apareçam ao lado de termos matemáticos, mas esta é apenas mais uma prova da natureza singular dessas complexas estruturas geométricas. Fractais talvez sejam uma das formas mais famosas de arte matemática existentes. Muitas vezes associados a estruturas caóticas, psicodélicas e enlouquecedoras, os fractais são fonte de admiração de um público cativado pela sua beleza hipnotizante ou pelas regras simples que dão vida a padrões complexos. Sem mais demoras, iremos agora entrar em um capitulo dedicado a essas formas intrigantes e ao espaço que elas conquistaram na arte computacional.
6.1 Autossimilaridade e recursividade
Fractais (do latim fractus: fração, quebrado) são padrões autossimilares ao longo de uma escala de ampliação infinita. Isso significa que fractais podem ser divididos em inúmeros outros pedaços que, se observados de perto, seriam idênticos ao fractal original. Curiosamente, fractais são encontrados em múltiplos fenômenos naturais, como flocos de neve (figura 6.1), raios, linhas costeiras, plantas (figura 6.2), montanhas, veias e padrões em animais dentre outros.

Olga Sytina e Alexey Kljatov.
a Todos os direitos reservados pelos artistas originais.

Scott Atwood.
b Todos os direitos reservados pelo artista original.
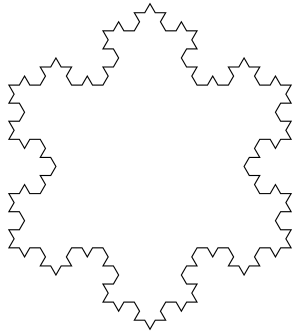
No segmento computacional, o floco de neve de Koch é um dos fractais em que se pode observar o comportamento autossimilar de forma mais evidente. Na imagem 6.4 é mostrada sua representação com sete níveis de subdivisões. Ele foi concebido como uma figura do tipo Scalable Vector Graphics e você pode aplicar um fator de ampliação relativamente alto a ela (mais de 5000%) para ver como o fractal se repete em escala macro e micro.
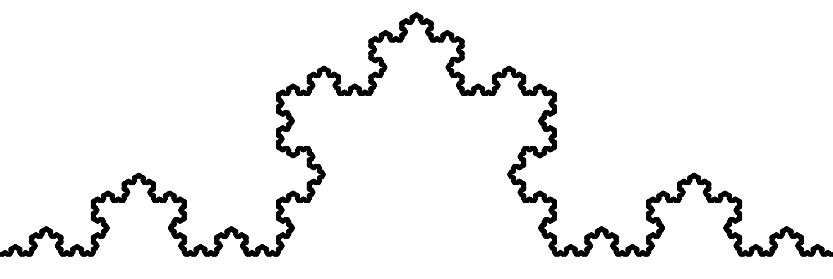
Os fractais mais notáveis são divididos em três grandes grupos. Os fractais geométricos, figura 6.5, são normalmente criados através de sucessivas repetições de um processo geométrico simples ao longo de um espaço indeterminado. O floco de neve de Koch é um fractal geométrico nascido a partir de uma regra de subdivisão infinita das retas que o compõe. Outros exemplos seriam os Triângulos de Sierpinski, a Árvore Fractal e a Curva Dragão.

Por outro lado, os denominados fractais abstratos, figura 6.9, como os criados por Mandelbrot, podem ser gerados através de computadores que calculam repetidamente uma equação matemática ou uma relação de recorrência. O Conjunto de Mandelbrot e o de Julia são os mais famosos deste tipo.

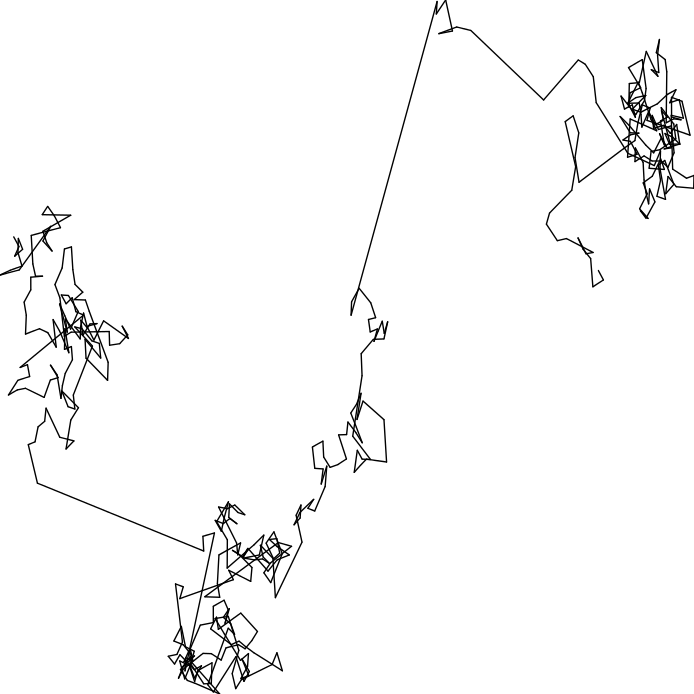
Por último, estão os fractais aleatórios, figura 6.12, formados através de processos estocásticos. Neste grupo estão o Voo de Lévy e as Trajetórias do Movimento Browniano.

Um fractal é criado pela repetição infinita, no âmbito espacial e temporal, de um padrão sobre si mesmo. Esse incessante empilhamento de operações e desenhos o torna ideal para ser materializado por um computador. As palavras chave quando nos referimos a essas figuras são recursividade e regras. A recursividade faz analogia a funções que realizam chamadas a elas mesmas. Por exemplo, uma linha de ação lógica de programação seria projetar uma função que desenhasse parte do padrão e, em seguida, fazer com que essa sub-rotina invocasse a si mesma, repetindo a forma e criando a autossimilaridade. É importante observar que enquanto essa repetição infinita é inofensiva na teoria, ela é muito perigosa na prática. Na maioria das vezes a recursividade multiplica o número de operações realizadas por iteração ou ciclo de desenho da figura. Quando programado, um fractal deve possuir uma condição de parada, caso contrário ele irá explodir no numero de operações e travar a simulação por falta de memória. As condições de parada da recursividade para um fractal normalmente se resumem a um tamanho visual mínimo, afinal, não faz sentido possuir um número infinito de detalhes se o computador não for capaz de exibí-los. Baseado nessa explicação simplificada, você pode ter concluído que a forma básica de uma função recursiva que desenha um fractal é algo do tipo:
Código 6.1 -
// 1) Desenha o padrão.
// 2) Gera novosArgumentos baseados em regras.
// 3) Função chama a si mesma com os novos argumentos.
if(condicaoDeParada == false) {
desenhaFractal(argumentos e/ou novosArgumentos);
}
}
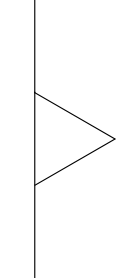
Igualmente importante são as regras ou os processos que dão vida a esses padrões. Os fractais geométricos são profundamente enraizados em regras simples repetidas ao longo de muitas iterações, gerando imagens de uma complexidade visual mesmerizante. Em geral essas regras se limitam a desenhar elementos geométricos (círculos, retas, retângulos, etc.), rotados e transladados, respeitando pré-condições de projeto. Um exemplo que podemos citar é do próprio floco de neve de Koch, cujas leis de construção, mostradas abaixo e ilustradas em 6.15, são baseadas na subdivisão recursiva de retas.
- Comece com um segmento de reta.
- Divida a reta em outros três segmentos de comprimentos idênticos.
- Desenhe um triângulo equilátero que possua o segmento central do passo 2 como base.
- Remova o segmento que é a base do triângulo desenhado no passo 3
- Repita os passos anteriores para cada segmento de reta existente.



Os detalhes em um fractal são revelados quando as regras de construção são repetidas para cada subelemento (passo 5 nas instruções citadas anteriormente), figura 6.21.

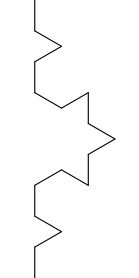
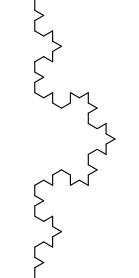
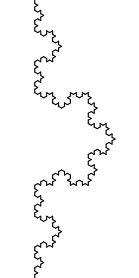
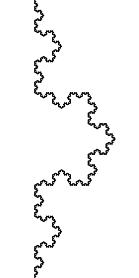
Você entenderá melhor como essas regras locais são capazes de gerar um resultado global quando programar um fractal nas próximas seções.
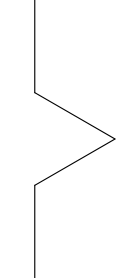
Um estudo de caso clássico, simples e belo é o fractal planta ou árvore. Ele recebe esse nome em homenagem a sua forma, que remete a de uma árvore composta por um tronco central que se desdobra em diversos galhos ou ramos a medida que ela cresce, figura 6.28.

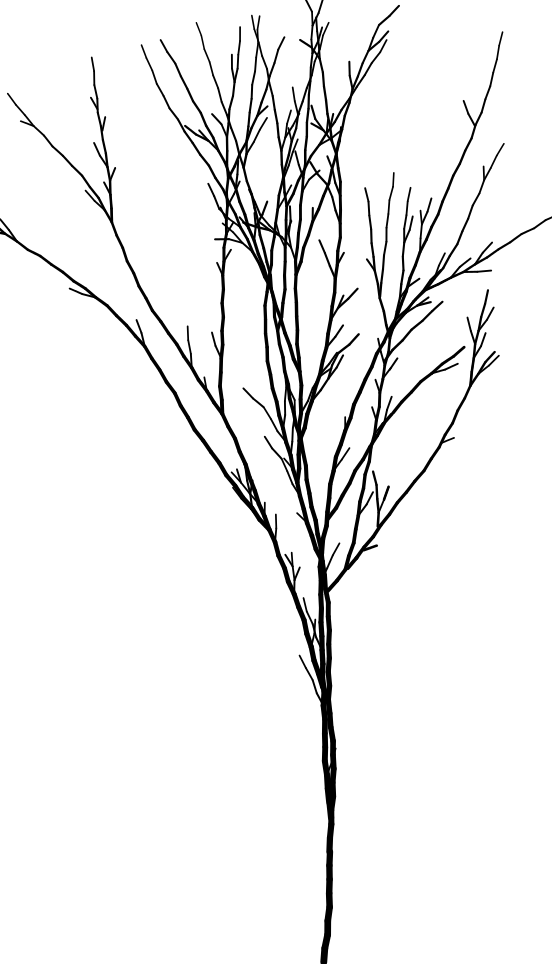
Ao final deste capítulo você será capaz de reproduzir formas como esta, mas primeiramente você deve começar pelo básico e entender como um fractal é transmutado do conceito para o código. Concentre-se na forma mais rudimentar de um fractal regular[2] desta categoria e como ele se desenvolve a cada iteração da recursividade, mostrados na figura 6.31.

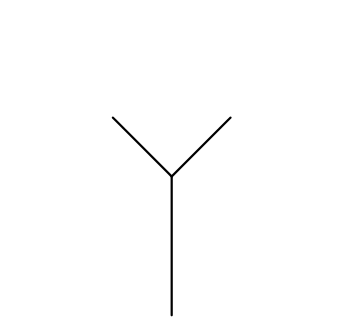
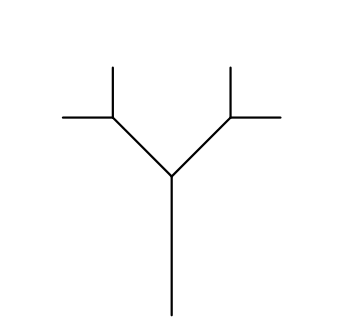
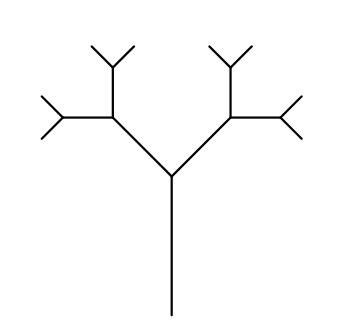
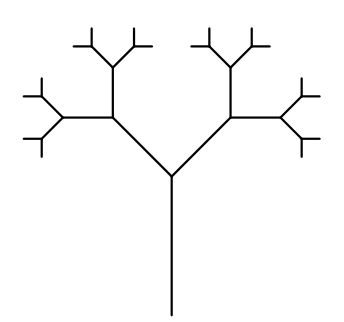
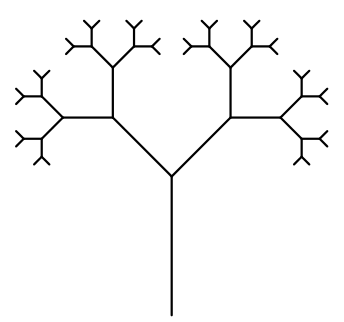
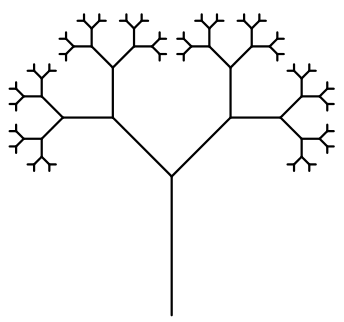
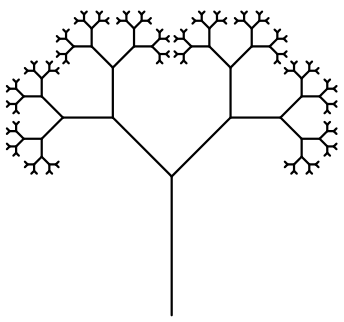
A análise do fractal através de etapas é mais naturalmente entendida se analisarmos apenas um único ramo da árvore, figura 6.40, uma vez que os demais são gerados por repetições simétricas da forma principal. Este ramo também será propositadamente distorcido de modo que a cada iteração o tamanho do próximo galho seja apenas ligeiramente menor que o anterior, como mostrado na figura 6.41. O objetivo é propiciar uma explanação mais clara da etapa geométrica de projeto do fractal.

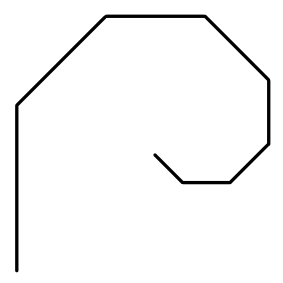
- Desenhar uma reta cujo ponto inicial é igual ao ponto final da reta da iteração passada.
- Inclinar a reta desenhada em 1, para que ela tenha um certo ângulo em relação à reta desenhada na iteração passada.
- Reduzir o tamanho da reta desenhada em 1, de forma que ela seja menor que a reta desenhada na iteração passada.
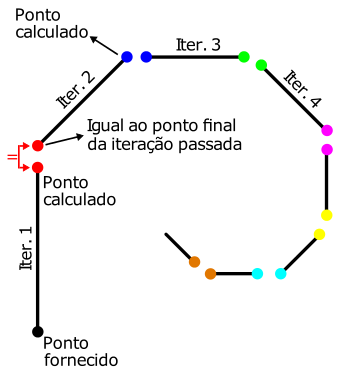
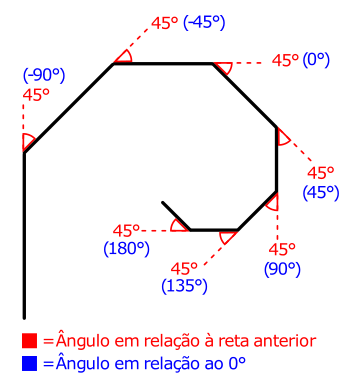
- Parâmetros da função: Deverão ser fornecidos, para cada iteração, um ponto inicial, um comprimento da reta e o ângulo de inclinação dessa reta, totalizando três argumentos de entrada.
- Corpo da função: Essa função calculará o ponto final da reta usando os argumentos de entrada e as equações trigonométricas do círculo (4.1). A reta que representa o ramo da árvore será traçada através da função line() usando as coordenadas do ponto inicial (fornecido) e final (calculado).
- Retorno da função: A função deverá devolver as coordenadas x e y do ponto final da reta para que essa informação seja usada na próxima chamada da sub-rotina (próxima iteração). Isto implica em mais de uma variável de retorno sendo necessário usar vetores para agrupar os dados.
Seguindo esse raciocínio você pode prontamente escrever a função para desenhar um ramo dessa árvore e depois chamá-la no programa principal:
Código 6.2 - Ramo simples -
size(500,500);
background(255);
float[] pontos = new float[2];
// Utilizado -90° apenas para que a árvore cresça para cima da tela.
pontos = arvore(width/2,height,100,-90);
}
float[] arvore(float _xi, float _yi, float _comp, float _angulo) {
// Fórmula básica mostrada na seção 4.1
float xf = _xi + cos(radians(_angulo))*_comp;
float yf = _yi + sin(radians(_angulo))*_comp;
line(_xi,_yi,xf,yf);
// Esta função retorna os pontos final do ramo:
float[] posFinal = {xf,yf};
return posFinal;
}
Código 6.3 -
// Iteração 1.
pontos = arvore(width/2,height,100,-90);
// Iteração 2: 60% menor e inclinado 45° em relação à Iteração 1.
pontos = arvore(pontos[0],pontos[1],100*0.6,-90 + 45);
// Iteração 3: 60% menor e inclinado 45° em relação à Iteração 2.
pontos = arvore(pontos[0],pontos[1],100*0.6*0.6,-90 + 45 + 45);
// Iteração 4: 60% menor e inclinado 45° em relação à Iteração 3.
pontos = arvore(pontos[0],pontos[1],100*0.6*0.6*0.6,-90 + 45 + 45 + 45);
Observe que essa abordagem não é elegante, uma vez que é necessário que a função arvore() retorne variáveis que serão usadas em chamadas posteriores dessa mesma função, além de ser requerida a atualização manual dos argumentos de entrada. Uma solução para esse problema é usar a recursividade. Perceba que a função arvore(), escrita dessa maneira, não é recursiva, ou seja, ela não faz uma invocação a si mesma. No entanto isso seria muito interessante dado que ela possuí todos os argumentos necessários para a execução da próxima iteração: o ponto final da reta anterior, o novo ângulo de inclinação e o novo comprimento. Vamos atualizar nossa função com essas sugestões, mas não execute esse novo código ainda!
Código 6.4 - Ramo recursivo -
// Fórmula básica mostrada na seção 4.1
float xf = _xi + cos(radians(_angulo))*_comp;
float yf = _yi + sin(radians(_angulo))*_comp;
line(_xi,_yi,xf,yf);
// Cada novo ramo será 60% do tamanho do original:
float novoComp = 0.6*_comp;
// Cada novo ramo será inclinado 45°do ramo anterior:
float novoAngulo = _angulo + 45;
// Recursividade: Esta função faz uma chamada
// a ela própria (com novos argumentos) para desenhar
// a próxima reta do ramo.
arvore(xf,yf,novoComp,novoAngulo);
}
A rotina acima irá desenhar uma figura como a 6.41, mas se você executá-la dessa maneira o Processing irá travar, com uma mensagem de erro igual a mostrada na figura 6.46, indicando um estouro de memória em virtude da recursividade infinita . Essa falha ocorreu porque em 6.4 existe um erro inerente de projeto visto que não foi adicionada uma condição de parada para impedir a repetição descontrolada da chamada da função. Isto é de suma importância no fractal árvore, pois ele cresce quadráticamente com o número de iterações. Em outras palavras, uma reta gera duas, que geram quatro, que geram oito e assim por diante, sempre dobrando o número de retas a cada iteração.
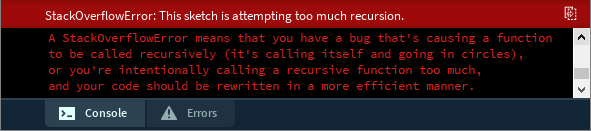
Um bom candidato para condição de parada é a resolução visual. Como cada reta que compõe o fractal diminui o seu tamanho a cada iteração, se esse tamanho for menor que certo valor, tal como 2 pixels, a função não será mais chamada recursivamente. Vamos aproveitar e fazer uma última alteração. Conforme mostrado na figura 6.31, cada iteração consiste em desenhar dois ramos (ou retas) com inclinações simétricas. Por exemplo, se um é desenhado com +45° o outro deverá ser desenhado com -45° . Podemos incluir essa simples condição e, em vez de fazer uma única chamada recursiva, fazer duas para que sejam desenhados dois ramos no final de cada iteração. Veja o código completo a seguir:
Código 6.5 - Árvore recursiva -
size(500, 500);
background(255);
arvore(width / 2, height, 100, -90);
}
void arvore(float _xi, float _yi, float _comp, float _angulo) {
// Condição de parada da recursividade:
// Comprimento do ramo menos que 2 pixels.
if (_comp > 2) {
// Cálculo do ponto final do ramo e seu desenho:
float xf = _xi + cos(radians(_angulo)) * _comp;
float yf = _yi + sin(radians(_angulo)) * _comp;
line(_xi, _yi, xf, yf);
// Cada novo ramo será 60% do tamanho do original:
float novoComp = 0.6 * _comp;
// São duas retas, uma inclinada a +45°da reta original
// e outra a -45°da reta original:
float novoAnguloR1 = _angulo + 45;
float novoAnguloR2 = _angulo - 45;
// Recursividade: Esta função faz duas chamadas
// a ela própria (com novos argumentos) para desenhar
// outras 2 retas.
arvore(xf, yf, novoComp, novoAnguloR1);
arvore(xf, yf, novoComp, novoAnguloR2);
}
}
Você pode perceber que não houve nenhuma mudança quanto a chamada da função em setup(), visto que todos os passos para desenhar o fractal estão contidos em arvore(). O fluxo de desenho também é mantido e conhecido: a primeira reta será desenhada no ponto central da parte inferior da tela, com um comprimento de cem pixels e uma angulação de -90°. Como dito anteriormente, esse ângulo foi definido de maneira que a árvore crescesse para cima. Se você alterar esse ângulo a árvore passará a ter uma inclinação diferente, mas seus ramos continuarão com uma inclinação de 45° em relação ao ramo originário e com 60% do tamanho do mesmo, já que tais características foram fixadas no corpo da função.
Claro que você deve estar imaginando como seria essa árvore se você alterasse os 45° para algum outro valor. Você pode investigar o resultado mudando essa grandeza diretamente no corpo da função, ou pode reescrevê-la para que ela contemple mais um argumento, sendo este o ângulo de inclinação dos ramos. O código abaixo produz resultados como os da figura 6.47.
Código 6.6 - Árvores fractais -
size(500, 500);
background(255);
}
void draw() {
background(255);
// Angulo do ramo vai de 0°a 180°
// de acordo com a posição horizontal do mouse:
float aRamo = map(mouseX, 0, width, 0, 180);
arvore(width / 2, height, 100, -90, aRamo);
}
void arvore(float _xi, float _yi, float _comp, float _angulo, float _anguloRamo) {
if (_comp > 2) {
float xf = _xi + cos(radians(_angulo)) * _comp;
float yf = _yi + sin(radians(_angulo)) * _comp;
line(_xi, _yi, xf, yf);
float novoComp = 0.6 * _comp;
float novoAnguloR1 = _angulo + _anguloRamo;
float novoAnguloR2 = _angulo - _anguloRamo;
arvore(xf, yf, novoComp, novoAnguloR1, _anguloRamo);
arvore(xf, yf, novoComp, novoAnguloR2, _anguloRamo);
}
}
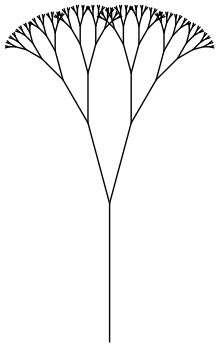
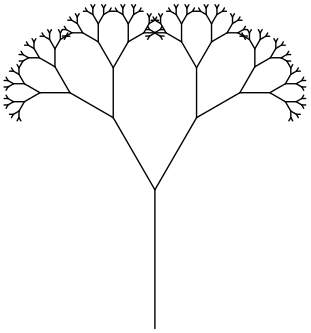
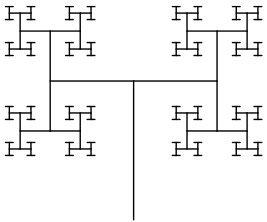
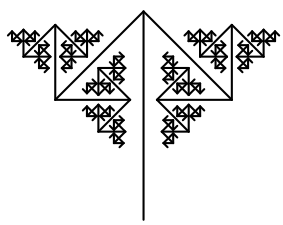
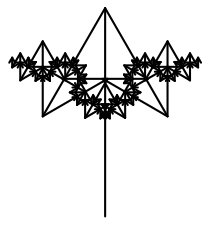
Finalizada a implementação da forma do fractal, podemos experimentar com variações sobre a função arvore() para criar efeitos artísticos. Muitos deles se resumem a modificar as variáveis da função original, mas irão ecoar em estéticas significativamente diferentes. No entanto, deve-se ter cuidado ao alterar esses coeficientes, pois isso pode acarretar em um aumento colossal de operações e travar a simulação. Em geral, uma boa prática é ajustar os coeficientes individualmente e alterar levemente seus valores, sempre observando quais são os efeitos gerados no fractal.
A primeira alteração que você pode fazer é reduzir o quanto um ramo será encurtado a cada iteração que, no código original, é de 40% em relação ao comprimento do ramo originário. Reduzir menos esse tamanho implica em mais repetições para que a condição de parada seja atingida, diretamente aumentando o número de ramos. Para realizar essa alteração basta modificar a linha que define essa redução. Os efeitos são mostrados na figura 6.53.
Código 6.7 -
float novoComp = 0.70*_comp;
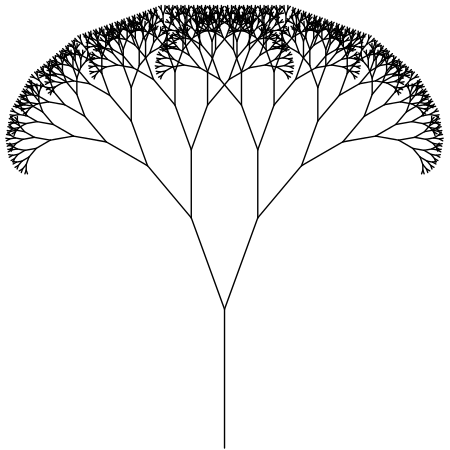
Outra característica marcante que pode ser modificada é a simetria do fractal. Podemos forçar um crescimento assimétrico ao criar dois fatores distintos de redução de tamanho do ramo, um para cada função recursiva. Veja na figura 6.54 que o fractal assume forma bem diferente da original. Retorne ao código 6.6 e altere as linhas internas a função arvore() de:
Código 6.8 -
arvore(xf,yf,novoComp,novoAnguloR1,_anguloRamo);
arvore(xf,yf,novoComp,novoAnguloR2,_anguloRamo);
para:
Código 6.9 -
float novoCompR1 = 0.8*_comp;
float novoCompR2 = 0.5*_comp;
arvore(xf,yf,novoCompR1,novoAnguloR1,_anguloRamo);
arvore(xf,yf,novoCompR2,novoAnguloR2,_anguloRamo);

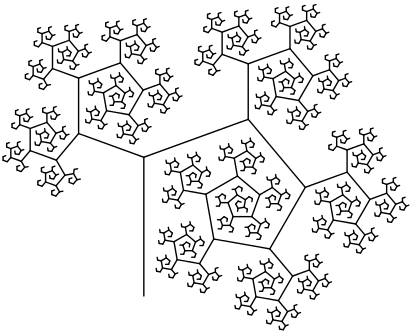
E se você quiser que o fractal se pareça realmente com uma árvore? Então seria preciso colocar "folhas" nas terminações de seus "galhos". Neste caso você deve lembrar que o fractal só atinge o último ramo após passar pela condição de parada. Consequentemente você pode adicionar um else no condicional para fazer com que ela desenhe um círculo que imitará uma folha. Veja a figura 6.57.
Código 6.10 -
if (_comp > 2) {
stroke(50);
strokeWeight(1);
float xf = _xi + cos(radians(_angulo)) * _comp;
float yf = _yi + sin(radians(_angulo)) * _comp;
line(_xi, _yi, xf, yf);
float novoComp = 0.6 * _comp;
float novoAnguloR1 = _angulo + _anguloRamo;
float novoAnguloR2 = _angulo - _anguloRamo;
arvore(xf, yf, novoComp, novoAnguloR1, _anguloRamo);
arvore(xf, yf, novoComp, novoAnguloR2, _anguloRamo);
}
else {
// Sumula uma "folha" como um círculo de tom esverdeado:
fill(random(100, 120), random(165, 185), random(130, 150), 10);
stroke(random(100, 120), random(165, 185), random(130, 150), 150);
strokeWeight(0);
float raio = random(25, 50);
ellipse(_xi, _yi, raio, raio);
}
}
Obviamente que poderíamos aumentar ainda mais a semelhança com uma árvore se a figura possuísse um tronco e galhos que se tornassem cada vez mais finos de acordo com seu tamanho. Essa alteração requer uma variável que esteja ligada as iterações do fractal, uma vez que mais iterações significam ramos mais distantes do ramo originário e, portanto, mais finos. Sabemos que a própria função arvore() possui um argumento de entrada relativo ao tamanho do ramo, que diminui conforme o fractal se expande. Sendo assim podemos vincular esse argumento à formatação da espessura da linha desenhada, simulando um afinamento da estrutura a cada ciclo. Os resultados podem ser vistos na figura 6.58.
Código 6.11 -
if (_comp > 2) {
// O comprimento vai de 100 a 2, e a espessura de 10 a 0.
// É necessário que a transformação seja decrescente
// para que ocorra o afinamento dos ramos.
float espessura = map(_comp, 100, 2, 10, 0);
strokeWeight(espessura);
float xf = _xi + cos(radians(_angulo)) * _comp;
float yf = _yi + sin(radians(_angulo)) * _comp;
line(_xi, _yi, xf, yf);
float novoComp = 0.65 * _comp;
float novoAnguloR1 = _angulo + _anguloRamo;
float novoAnguloR2 = _angulo - _anguloRamo;
arvore(xf, yf, novoComp, novoAnguloR1, _anguloRamo);
arvore(xf, yf, novoComp, novoAnguloR2, _anguloRamo);
}
}
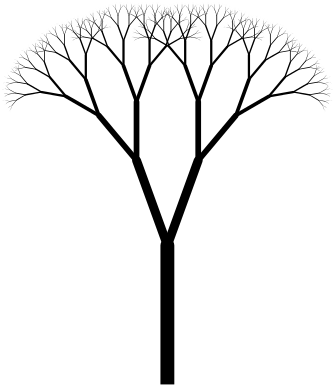
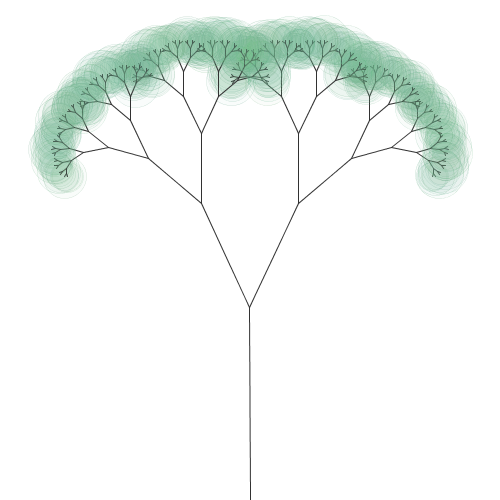
Todas as formatações apresentadas contribuem para uma exibição que emula o natural, mas a forma principal ainda pode ser retraçada a sua origem estruturalmente mecânica. O recurso final para combater esse excesso de rigidez é aplicar os conceitos do capítulo 4 relativos a aleatoriedade. O caos pode ser usado para quebrar os alicerces simétricos e regulares dos fractais, criando formas mais orgânicas. A autossimilaridade perfeita será perdida, mas a definição é abrangente o suficiente para incluir aproximações das formas. O procedimento para aplicar a incerteza é idêntico ao das seções passadas: identificar um ponto que influencie consideravelmente o desenho de nossa figura e torná-lo aleatório. Em nosso exemplo em específico, a angulação dos ramos é a candidata perfeita. Simplesmente edite a parte abaixo do código:
Código 6.12 -
float novoAnguloR2 = _angulo - _anguloRamo;
para:
Código 6.13 -
float novoAnguloR2 = _angulo - random(_anguloRamo);
Antes de executar seu novo programa, tenha certeza de mover a chamada da função arvore() para dentro de setup() (ou seja, remova-a de dentro do draw()). Isso é especialmente importante, caso contrário a cada frame será gerado um número aleatório e a sua árvore vai parecer que está se movimentando muito rápida e irregularmente. A figura 6.59 apresenta um fractal sob o efeito de perturbações caóticas.

Diversas outras ideias podem ser usadas para incrementar os fractais, como múltiplas exibições simétricas, irregularidades na angulação dos ramos, inclinações exacerbadas ou irrisórias, dentre outras. Combinando-as com as algumas das técnicas apresentadas nesta seção, você pode gerar padrões realmente complexos e surreais que não parecem ter sido desenhados por regras simples, como é o caso do fractal árvore. Essa filosofia foi empregada para gerar figuras como a 6.60 ou 6.61. Note que, no sentido fiel da palavra, essas figuras não são fractais e sim obras gerativas nascidas de instruções recursivas.


Neste capítulo você aprendeu um pouco mais sobre o que são as curiosas estruturas autossimilares denominadas fractais. Sua beleza hipnotizante é tanto derivada da figura macro do fractal quanto da repetição infinita de regras e frações simples. Na parte que aludiu à programação você viu que a recursividade computacional consiste na chamada de uma função dentro si mesma, sendo a chave para criar a autossimilaridade dos fractais.
No quesito prático, você acompanhou um passo a passo do projeto de um fractal, incluindo como derivar as regras de desenho e condições de parada da recursividade. Por último, foram mostradas múltiplas maneiras de se utilizar formatações para conceder um estilo único em sua imagem, ou adicionar variedade a sua arte.
[1] Mandelbrot, B. B. (1989). "Fractal Geometry: What is it, and What Does it do?". Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences 423(1864).
[2] Não perturbado por funções do tipo noise() ou random().