[ CAPÍTULO 4 ]
Ordem
A essência da realidade
A obsessão da humanidade em ordenar o mundo e responder a perguntas sobre a vida, o universo e tudo mais, a impulsionou a inventar[1] a mãe de todas as invenções, a matemática. Ela é tão absurdamente necessária na civilização moderna que está integralmente presente em todas as áreas que compõem nossa sociedade. Na física ela é a base para formalizar conceitos que se estenderem desde as menores partículas da mecânica quântica até as mais colossais estrelas do cosmos. Na química ela auxilia a entender a formação de elementos da tabela periódica assim como prever taxas em mecanismos de reações. Na biologia ela é responsável por modelos capazes de predizer ou descrever ocorrências naturais, como comportamentos e padrões de organismos ou mudanças populacionais. Muito abstrato para você? Então lembre-se que ela é a base do nosso sistema financeiro e usada sempre que você precisa seguir uma receita ou dizer as horas. Resumindo, é ela quem permite modelar os segredos e as belezas do universo através das ciências.
Curiosamente, a matemática por si própria, pura, contém muitas belezas que costumam passar despercebidas por nós. Existem aquelas relacionadas com o método e que remetem à simplicidade ou multiplicidade de provas, como é o caso do célebre Teorema de Pitágoras. Outras derivam de conexões entre diferentes áreas da matemática, tal qual a Equação de Euler, considerada a equação mais notável da matemática pelo físico Richard Feynman. Há, ainda, aquelas ligadas diretamente aos números, como a perpétua constante π ou a sequência de Fibonacci.
A estética, na programação artística, se apoia vigorosamente em um tipo de beleza mais direta e visual, proveniente de imagens, quase que místicas, nascidas de um amálgama de números e fórmulas. Felizmente, os artifícios empregados para essa tarefa passam longe do reino do esoterismo, sendo fortemente enraizados em diversas áreas da matemática. Neste capítulo você será convidado a mudar um pouco a sua visão sobre a matemática e entender como você pode domá-la, reinterpretando conceitos para aplicações relacionadas à arte gerativa. Você aprenderá como algumas fórmulas simples possuem vastas aplicações na computação e em sua vertente artística.
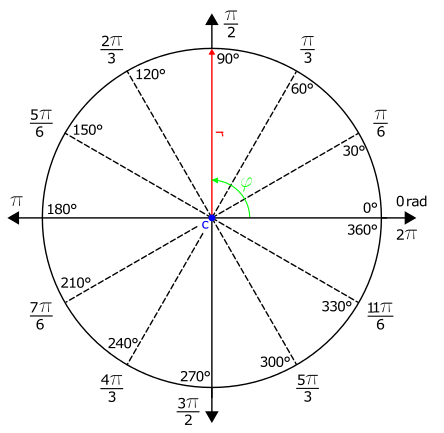
Vamos começar com um conceito cuja origem pode ser traçada há cerca de quatro mil[2] anos atrás com duas civilizações à frente de seu tempo. Os egípcios, fascinados pela forma piramidal, construiram tumbas monolíticas que, a olhos desatentos, parecem apenas um aglomerado de pedras empilhadas. No entanto a descoberta de documentos[3] datados da época do império médio dos egípcios revelaram fórmulas matemáticas, sugerindo que os mesmos cortavam essas grandes estruturas em triângulos e calculavam múltiplas propriedades geométricas, em especial o Seked um análogo à moderna cotangente de ângulos. A segunda civilização, a Babilônica, registou, em uma coleção de tábuas de argila, conceitos relativos à matemática, sendo parte destinada a geometria e cálculos de áreas de triângulos e volumes de prismas. Astrônomos babilônicos documentavam, com detalhes, informações acerca de eclipses lunares, solares, movimentações planetárias e de estrelas, incluindo predições sobre as mesmas[4]. Esses estudos antigos, em grande parte empíricos e voltados para um objetivo prático, seriam futuramente aperfeiçoado pelos gregos, formalizando a universal trigonometria , uma área da matemática que investiga relações envolvendo comprimentos e ângulos em triângulos. Ela possui aplicações na arquitetura, acústica, arte, música, eletrônica, estatística, astronomia, cinema e inúmeros outros segmentos. Nesta seção você será direcionado a focar em uma pequenina parte do todo, relacionada ao estudo de triângulos e desenhos de círculos e demais figuras geométricas.
Você deve se lembrar que no Processing existe a função ellipse() para desenhar círculos por completo, mas nós não estamos interessados exatamente nele. Nossa atenção deve ser voltada para os infinitos pontos que compõem a figura. As informações relativas as coordenadas x e y desses pontos podem ser obtidas através de relações trigonométricas e usadas para tarefas como criação de padrões visuais. Não se preocupe se você não se lembrar desses conceitos, vamos aplicar apenas a trigonometria básica, e quando digo básica, significa do ensino médio, não mais que isso. Começaremos pelo objeto de estudo, o círculo, que é uma figura fechada da geometria Euclidiana, composto pelas coordenadas cartesianas de seu centro (c) e o tamanho de seu raio (r). Para desenhar um círculo basta imaginar uma reta iniciada no ponto central, cujo comprimento é igual ao raio, e depois girar[5] essa reta 360° em torno desse ponto. Ele é ilustrado na figura 4.1.
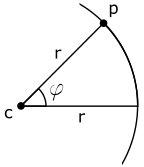
Por outro lado, se em vez de completar 360° para gerar um círculo, você girar um ângulo qualquer, representado pela letra grega fi (φ), você terá um arco dele, como o da figura 4.2. Nosso principal objetivo é encontrar as coordenadas dos infinitos pontos localizados na superfície ou borda do círculo. Isso pode ser feito se traçarmos triângulos dentro do arco formado pelos pontos de interesse da figura, veja a imagem 4.3.
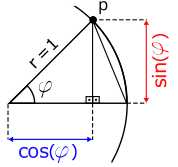
Após manipulações matemáticas usando as funções seno e cosseno, obtemos as equações [6] que fornecem as posições x e y de qualquer ponto localizado na superfície de um círculo.
Código 4.1 - Equações do Círculo -
// extremidade de um arco de ângulo "theta" graus de um círculo de
// centro (centroX,centroY) e raio r.
x = centroX + raio*cos(angulo);
y = centroY + raio*sin(angulo);
Estas equações, apesar de matematicamente simples, são muito poderosas como você irá ver. Antes de colocá-las em prática existe um último ponto que você deve saber. As funções sin() e cos() do Processing trabalham com ângulos em radianos em vez de graus. A transformação entre essas duas grandezas é feita através da fórmula abaixo:
Felizmente o Processing nos ajuda com a função radians() que faz a conversão de graus para radianos. Finalmente, unindo o que foi explicado, você pode desenvolver um código para desenhar um círculo parametrizado, usando fórmulas em vez de uma função. Na teoria, um círculo é composto de infinitos pontos, mas na prática isso é inviável dado que o computador é um sistema digital discreto. Contornaremos essa limitação dividindo o círculo em um número arbitrário de pontos que serão conectados através de retas, código 4.2.
Código 4.2 - Círculo Paramétrico -
size(200,200);
background(255);
// Coordenadas dos centro de círculo e valor do raio:
float centroX = 100, centroY = 100;
float raio = 50;
// O círculo será desenhado através de linhas, precisamos dos pontos anteriores:
float xAnterior = centroX + raio*cos(0);
float yAnterior = centroY + raio*sin(0);
// Número de pontos que irão compor o círculo:
int div = 5; // Pentágono
//int div = 10; // Decágono
//int div = 50; // Pentacontágono
// Círculo parametrizado:
for(int i = 0; i < div + 1; i++) {
// Equações do círculo:
float x = centroX + raio*cos(radians(i*360.0/div));
float y = centroY + raio*sin(radians(i*360.0/div));
line(x,y,xAnterior,yAnterior);
xAnterior = x;
yAnterior = y;
}
// Círculo pelo Processing:
noFill();
stroke(0,40);
strokeWeight(2);
ellipse(centroX,centroY,2*raio,2*raio);
}
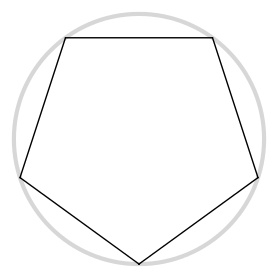
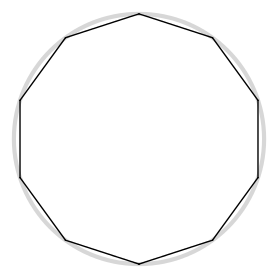
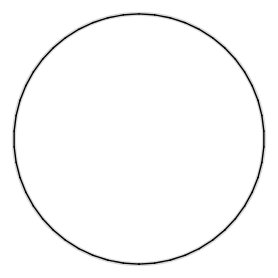
Neste código usamos a estratégia de dividir o desenho do círculo em setores, cada um com um tamanho de arco que depende da variável div, sendo marcado por um ponto na superfície da figura. Perceba que quanto maior da divisão do círculo, figura 4.8, que equivale a um passo menor no ângulo dos arcos, mais ele se parece com um círculo em vez de outro polígono regular. Cinco divisões geram um pentágono, enquanto cinquenta divisões criam um pentacontágono (50 lados) que, na prática, é uma ilusão de um círculo perfeito.
Desenhar círculos através de fórmulas matemáticas é algo incrível, pois mostra como é possível transcrever uma forma natural em uma estrutura rigorosamente numérica. Por outro lado, do ponto de vista artístico, essas figuras não trazem nada de inovador... ainda. A mágica acontece quando conceitos simples são utilizados de uma maneira não convencional e inesperada, e é assim que começamos de fato a mergulhar na programação artística. Para ilustrar essa ideia vamos fazer um pequeno exercício mental ou, se você preferir, faça no papel:
Imagine um círculo que é desenhado ponto a ponto até completar os 360°, conforme visto no código 4.2, mas apenas um ponto por frame de animação. Agora imagine um segundo círculo desenhado dessa mesma forma, mas a partir de um ponto defasado de 180° do primeiro e com a metade do tamanho do passo dele. Por último, visualize uma reta ligando esses dois pontos desenhados quadro a quadro. Esse processo é demonstrado na imagem 4.9. Que figura final você formará quando ligar todos os pontos desses dois círculos?
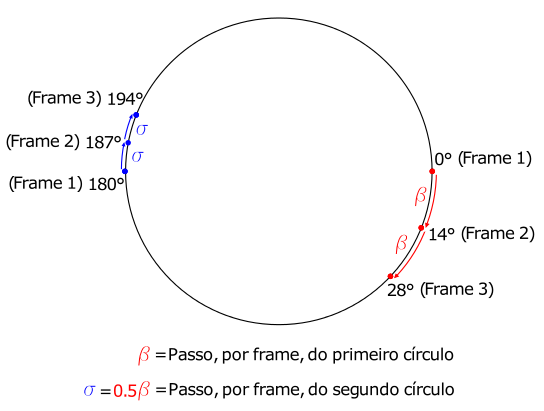
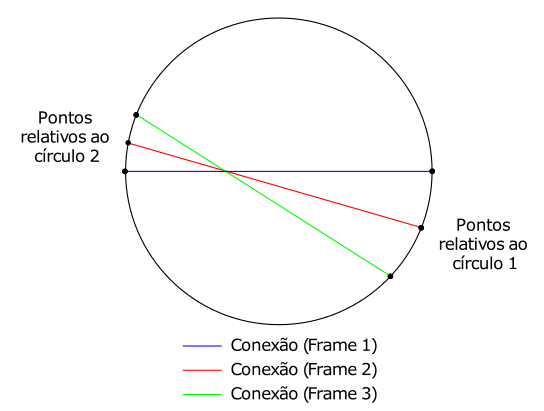
Você deve ter percebido que é muito difícil imaginar o resultado e isso ocorre simplesmente porque somos humanos. Este exercício exige uma capacidade de abstração imensa, assim como de memória para gravar o que acontece a cada quadro ou a cada novo ponto que é desenhado. Mas veja que, conceitualmente, este é um exercício simplório e que retas ligando círculos não devem produzir nada de fantástico, apenas retas, correto? Pois bem, você pode tirar a dúvida escrevendo um programa que desenha exatamente a atividade proposta. A janela de saída está mostrada na figura 4.12.
Código 4.3 - Conectando dois círculos -
size(400,400);
background(255);
// Diminui o número de quadros por segundo para 20.
frameRate(20);
}
void draw() {
float centroX = 200, centroY = 200;
float raio = 160, vel = 0.5;
int div = 50;
// Passo, ou quantos graus serão "andados" por frame do Processing:
float passo = 360.0/div;
// Primeiro Círculo:
float x1 = centroX + raio*cos(radians(frameCount*passo));
float y1 = centroY + raio*sin(radians(frameCount*passo));
// Segundo Círculo - Defasado 180°e animado com metade do passo do primeiro:
float x2 = centroX + raio*cos(radians(180 + vel*frameCount*passo));
float y2 = centroY + raio*sin(radians(180 + vel*frameCount*passo));
strokeWeight(2);
// Pontos vermelhos: Círculo 1.
stroke(255,0,0);
point(x1,y1);
// Pontos azuis: Círculo 2.
stroke(0,0,255);
point(x2,y2);
// Conexão entre os pontos dos dois círculos:
strokeWeight(0);
stroke(0,255,0);
line(x1,y1,x2,y2);
}
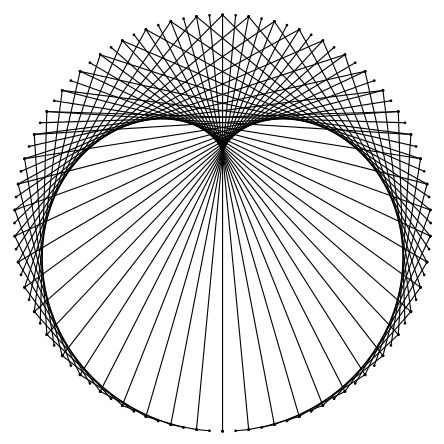
Neste código, a função draw() é responsável por desenhar apenas um ponto de cada círculo por frame. O grande auxiliador nesse processo é a variável frameCount , que é automaticamente e continuamente incrementada uma vez que contém o número de frames decorridos desde o início da execução do programa. Outros padrões são prontamente construídos se alterarmos o valor da velocidade de rotação ou raio de um dos círculos, exemplificados na figura 4.13.
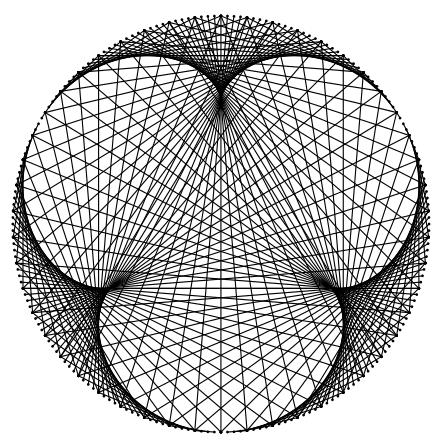
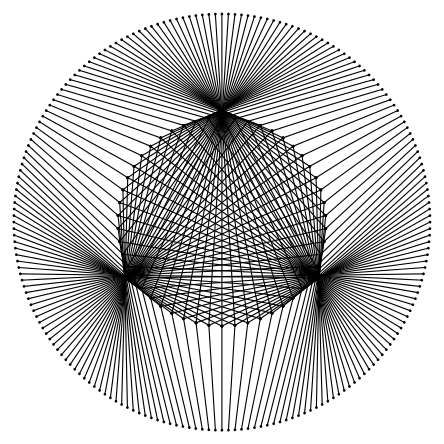
Com base nas figuras geradas podemos concluir que a combinação de conceitos simples pode resultar em algo muito mais complexo do que aplicá-los de maneira separada. Em nosso estudo de caso em específico isso é ilustrado pelas imagens hipnotizantes em forma de mandala geradas pelas regras que estabelecemos. A beleza matemática desse e de outros padrões desenhados dificilmente poderia ser prevista e, se fosse desenhada à mão, levaria um longo tempo para ser completada. São necessários um total de 150 pontos e 100 retas para desenhar a figura 4.12, sem contar o tempo para marcar os pontos de divisão do círculo. O computador é capaz de completar esses passos em décimos de segundo se não for necessário animar a tela. Esta é a grande vantagem de usar a computação para experimentar com a arte. Os padrões podem ser gerados, repetidos e alterados de maneira rápida e com um custo insignificante.
4.2.1 Pequenos acidentes favoráveis
O famoso pintor Bob Ross, adorado por fãs dentro e fora da internet por sua calma e seu estilo de pintura prática, casualmente pronunciava a frase "happy little accidents" [7] sempre que pincelava de uma maneira "errada". Nesse momento pessoas que assistiam a seus vídeos se contorciam em desespero, acreditando que pintura estaria arruinada. Com uma calma digna de um mestre Zen, Bob subvertia esses acidentes e inventava uma maneira de corrigir o erro, pintando um outro objeto no lugar ou aplicando um efeito inesperado na paisagem.
Na programação artística podemos traçar um paralelo dessa mentalidade no sentido que erros , nem sempre são erros, e sim uma maneira de explorar novas ideias que antes não haviam sido pensadas. Por exemplo, os padrões gerados na seção passada são altamente precisos no contexto em que você programou uma reta que conecta a coordenada x do círculo 1 com a do círculo 2 e a coordenada y do círculo 1 com a do círculo 2. Mas e se você tivesse cometido um erro e na hora de digitar você, equivocadamente, trocasse os pontos ou índices, sua arte estaria arruinada? Novamente, uma vantagem da programação é que você pode testar essas ideias de maneira ágil e com recursos e custos de implantação materialmente irrisórios: o seu tempo e criatividade. Se você não gostar, basta alterar uma única linha de código para desfazer o que você fez. Para ilustrar esse conceito, localize as linhas abaixo no código 4.3:
Código 4.4 -
point(x2,y2);
line(x1,y1,x2,y2);
E altere para um dos casos abaixo:
Código 4.5 -
point(x1,y2);
point(x2,y1);
line(x1,y2,x2,y1);
ou
Código 4.6 -
point(x1,x2);
point(y1,y2);
line(x1,x2,y1,y2);
Os padrões gerados estão mostrados nas figuras 4.16 e 4.17. Perceba como mudanças muito pequenas, como a simples troca de duas variáveis, causam impactos significativos no comportamento do programa. No caso deste exemplo são geradas novas variantes de padrões impossíveis de serem reproduzidas apenas alterando a posição inicial dos círculo ou o tamanho do passo, por frame, do ângulo. Esta é uma lição que demonstra perfeitamente que mesmo erros podem ser usados como fonte de aprendizado, aperfeiçoamento e inspiração.

girado em 90°.
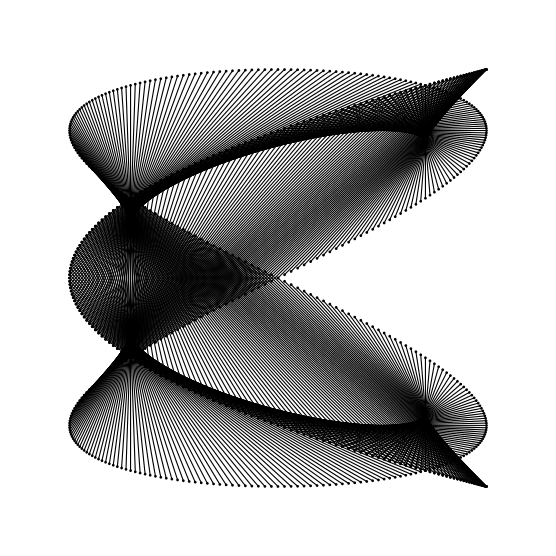
girado em 90°.
Uma das classes de figuras provenientes da trigonometria são aquelas que apresentam a elegante simetria radial. Tal característica indica que um corpo pode ser cortado por um ou mais planos longitudinais que, quando atravessam seu centro, o dividem em partes iguais. Ao girar essa parcela em torno de um ponto central, ela é capaz de reconstruir o objeto original. Essas formas são abundantemente encontradas na natureza em animais, flores e frutas, veja a seção de uma laranja na figura 4.18.


As equações 4.1 foram batizadas como as equações do círculo, mas elas também podem ser usadas para desenhar uma variedade de figuras que apresentam esse tipo de simetria. Isso se deve ao fato delas serem desenhadas nos 360° em torno de um ponto central, semelhante a um círculo. Uma estrela por exemplo, imagem 4.20, é uma figura radialmente simétrica.


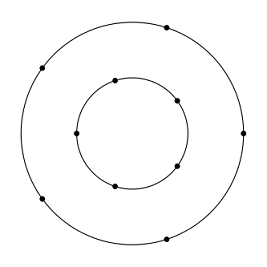
A estrela é formada por dez pontos, dos quais alguns estão na borda de um círculo externo de raio re e outros estão na parte interna, em um círculo cujo raio ri é a metade do valor do primeiro. Você pode escrever um código para desenhar essa disposição de pontos utilizando uma estrutura de repetição semelhante a usada no início deste capítulo para desenhar um círculo. No entanto será preciso incluir um condicional para alternar o desenho dos pontos entre o círculo externo e interno. Sempre que um ponto for desenhado com raio re, o seguinte será desenhado com ri. O código a seguir dispõe os pontos como na figura 4.21 e depois os conecta.
Código 4.7 -
size(300, 300);
background(255);
// Coordenadas dos pontos que compõem a estrela de 5 vértices:
float[] x = new float[10];
float[] y = new float[10];
for (int i = 0; i < 10; i++) {
float r = 0;
// Se o ponto for par temos o raio externo, se ímpar, o interno:
if (i % 2 == 0) {
r = 100;
}
else {
r = 50;
}
x[i] = width / 2 + r * cos(radians(i * 36));
y[i] = height / 2 + r * sin(radians(i * 36));
}
// Desenho da estrela - Conecta, sequencialmente, os pontos gerados:
for (int i = 1; i < 10; i++) {
line(x[i - 1], y[i - 1], x[i], y[i]);
}
// A última ligação deve ser feita fora da repetição,
// unindo o primeiro com o último ponto:
line(x[0], y[0], x[9], y[9]);
}
O condicional que testa se a variável i é par ou ímpar já foi explicado na seção 2.5.2, e é reutilizado aqui, pois sequencialmente sempre existirá um número ímpar depois de um par. Como queremos que seja desenhado, alternadamente, um ponto com raio re e outro com raio ri, é conveniente utilizar essa estratégia para posicionar os pontos.
Agora que o conceito de figuras radiais foi desmistificado, é possível incorporar algumas funcionalidades para deixá-las menos triviais. O primeiro passo é a parametrização das variáveis que mais impactam na forma da figura, como o número de vértices da estrela e os raios internos e externos dos círculos que a compõem. Isso permite adicionar variedade as formas com um simples mudar de valores, de uma maneira rápida e simplificada. O segundo ponto é animar a exibição da estrela através de um movimento de giro que, em uma figura radial, consiste em incrementar, quadro a quadro, o ângulo de todos os pontos que são desenhados. A velocidade de giro será diretamente proporcional ao incremento desse ângulo e, durante a execução, todos os pontos serão afetados, criando a ilusão de movimento da figura. Veja a implementação dessas funcionalidades no código abaixo e os resultados na figura 4.24.
Código 4.8 - Estrela animada -
int pontas = 6, nbr = 2 * pontas;
// Raio externo e interno:
float re = 100, ri = 0.5 * re;
// Giro da estrela (animação):
float incremento = 0;
void setup() {
size(300, 300);
background(255);
}
void draw() {
background(255);
// Coordenadas dos pontos que compõem a estrela:
float[] x = new float[nbr];
float[] y = new float[nbr];
for (int i = 0; i < nbr; i++) {
float r = 0;
// Se o ponto for par temos o raio externo, se ímpar, o interno:
if (i % 2 == 0) {
r = re;
}
else {
r = ri;
}
x[i] = width / 2 + r * cos(incremento + radians(i * 360.0 / nbr));
y[i] = height / 2 + r * sin(incremento + radians(i * 360.0 / nbr));
}
// Desenho da estrela - Conecta, sequencialmente, os pontos gerados:
for (int i = 1; i < nbr; i++) {
line(x[i - 1], y[i - 1], x[i], y[i]);
}
// A última ligação deve ser feita fora da repetição,
// unindo o primeiro com o último ponto:
line(x[0], y[0], x[nbr - 1], y[nbr - 1]);
// Aumenta o ângulo de incremento para criar a ilusão de giro da figura:
incremento += 0.01;
}


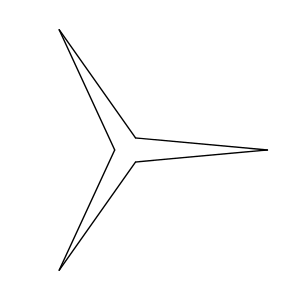
A animação pode se tornar mais dinâmica se você alterar de modo desproporcional características que mudem significativamente a forma da figura. Experimente incrementar gradativamente o ângulo de desenho de todos os pontos internos ou externos da estrela. Realizar essa soma apenas quando i é par ou ímpar é uma maneira de se obter este efeito. Substitua as linhas:
Código 4.9 -
y[i] = height/2 + r*sin(incremento + radians(i*360.0/nbr));
por:
Código 4.10 -
y[i] = height/2 + r*sin(incremento + radians(i*360.0/nbr + (i%2)*frameCount));
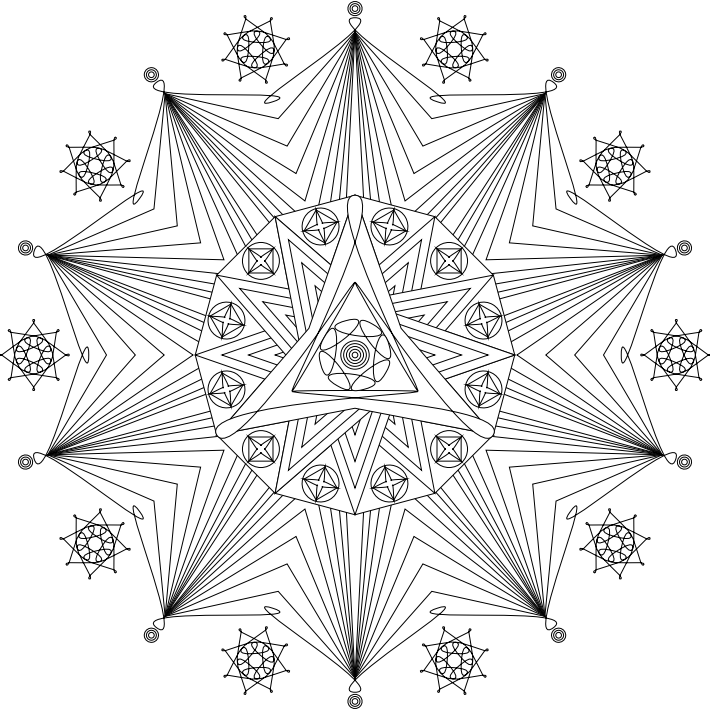
Usando somente derivações do código 4.8 você é capaz de criar uma quantidade surpreendente de figuras cuja variedade pode ser multiplicada se você utilizar números negativos em raios e defasagens em ângulos ou conectar os pontos através de curvas em vez de retas. Os resultados de parte dessas ideias são mostrados na figura 4.28. Combinando todas essas estratégias e sobrepondo figuras radiais você pode criar padrões similares à mandalas, veja a figura 4.29.




Aproveitando a caráter "circular" deste capítulo, existe mais uma forma inspirada na natureza que devemos estudar, a espiral. Diferentemente do que se possa imaginar, o principal propósito da espiral não é a estética, é a eficiência[8]. Essa estrutura é responsável por minimizar custos de voo de caça em falcões[9] ou maximizar a densidade de sementes em plantas[10]. Entretanto nada nos impede de apreciar os belíssimos espécies vegetais e animais que a tomam emprestada, figura 4.34.


a Todos os direitos reservados pelo fotógrafo original.
Analisando esse padrão tecnicamente percebemos que ele se difere de um círculo uma vez que é composto por um serpenteamento duradouro em torno de um ponto central. Isso nos leva a concluir dois fatos, que o "raio" de uma espiral não é fixo, continuamente crescendo (ou decrescendo) a cada volta da figura, e que ela requer múltiplas revoluções em torno do ponto central, ultrapassando o intervalo de 0° a 360° do círculo. Este último ponto é facilmente contornado, já que as funções seno e cosseno são periódicas e se repetem a cada 360°. Matematicamente temos que o valor do seno ou do cosseno de um ângulo qualquer será absolutamente igual ao desse ângulo somado a um múltiplo inteiro de 360°. Por exemplo, o seno de 30° é igual ao de 390° (30°+ 360°) ou 750° (30°+ 720°) ou, generalizando, 30°+ n*360° (onde n é um número inteiro), veja a figura 4.37.

Quando desenhamos um círculo evitamos ultrapassar esse limite, pois estaríamos revisitando uma área desenhada anteriormente no intervalo de 0° a 360°. Entretanto, essa propriedade é muito poderosa e permite que contornemos infinitamente um ponto central, justamente uma das necessidades para transformar o desenho de um círculo em uma espiral. Para completá-la, impomos a condição de aumentar progressivamente o raio original do círculo, impedindo permanentemente o fechamento da forma. O código abaixo gera a figura 4.38.
Código 4.11 -
size(300, 300);
background(255);
// Raio inicial e ângulo girado a cada iteração:
float r = 0, passo = 5, numVoltas = 15;
// Número de repetições:
float numRep = 360 * (numVoltas / passo);
float x, y, xa = width / 2, ya = height / 2;
for (int i = 0; i < numRep; i++) {
x = width / 2 + r * cos(radians(i * passo));
y = height / 2 + r * sin(radians(i * passo));
line(xa, ya, x, y);
xa = x;
ya = y;
r += 0.1;
}
}
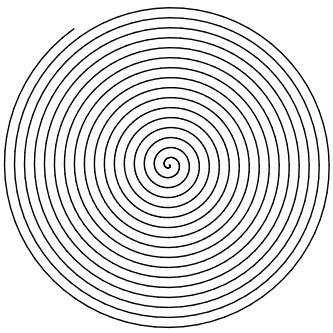
Vamos finalizar esta seção unindo nossas equações matemáticas determinísticas com o acaso não determinístico do capítulo passado. A escolha do "onde" [11] exatamente inserir o aleatório não é padronizável, mas por certo podemos analisar nossas equações e experimentar aplicá-lo em parâmetros que causarão grande impacto na imagem final. Para o caso de figuras radiais, uma possibilidade é decidirmos que queremos uma imagem sempre centrada e com passos regulares de ângulo para manter uma consistência na visualização. Segundo as equações trigonométricas 4.1, isso significa manter as variáveis centroX, centroY e angulo fixas. O único fator restante para atuar é no raio do círculo. Utilizando o código anterior como base, nossa espiral pode ser transformada para uma configuração mais rebelde, como as das figuras 4.39 e 4.40. Altere as linhas:
Código 4.12 -
y = height/2 + r*sin(radians(i*passo));
usando a função random() para gerar um efeito turbulento:
Código 4.13 -
y = height/2 + random(0.9,1.1)*r*sin(radians(i*passo));
ou noise() para um mais natural:
Código 4.14 -
y = height/2 + 1.5*noise(i/30.0)*r*sin(radians(i*passo));

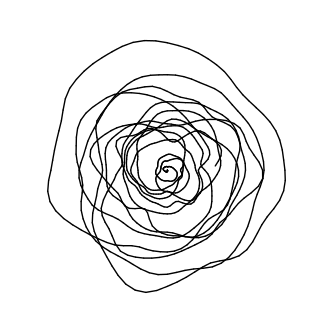
Perceba como entrelaçar da ordem e do caos é simbiótico ao se alimentar da complementariedade de cada uma das partes. As equações matemáticas fornecem a base, ou a forma geral da figura, e a aleatoriedade contribuí ao infiltrar o gerativo naquilo que seria predeterminado. O resultado é uma estrutura medular com incontáveis detalhes que se alteram cada vez que ela é gerada.

b Todos os direitos reservados pela instituição.
A trigonometria pode ser aplicada em uma série de tarefas na computação. O foco deste capítulo foi apresentar as poderosas equações paramétricas do círculo que, dentre outras aplicações, são usadas para desenhar polígonos regulares, figuras radiais e ainda espirais. É importante que você se familiarize e entenda, principalmente do ponto de vista geométrico, o que é possível realizar com as funções seno e cosseno. Adicionando a aleatoriedade aos códigos, geramos imagens erráticas, mas estruturadas, reforçando o papel do acaso no conjunto da obra.
No próximo capítulo é mostrado como empregar a formatação de maneira inteligente para enriquecer as exibições criadas por você em seus programas. Também será exemplificado como fundir todos os conceitos explicados até o momento para criar um projeto gerativo completo.
[1] Como o próprio nome sugere, a matemática é um estudo, um aprendizado. A questão principal sobre a origem da matemática, se ela é um constructo humano ou uma verdade universal, é um debate filosoficamente interminável que facilmente incorpora a tríade composta pelas ciências naturais, sociais e humanas. A palavra "inventar" foi escolhida apenas por conveniência.
[2] Reves, G. E. (1954). "Outline of the history of trigonometry". School Science and Mathematics 53(2): pags.87-171.
[3] Papiro de Rhind e Papiro de Moscou
[4] Maor, Eli (1998). "Trigonometric Delights". Princeton University Press, New Jersey. ISBN-13: 978-0-69-115820-4
[5] Na matemática convencional os ângulos crescem de valor no sentido de giro anti-horário, enquanto no Processing isso se sucede no sentido horário.
[6] Estas talvez sejam as fórmulas mais importantes apresentadas neste livro. Elas são definidas como equações do círculo, mas podem ser usadas para modelar eventos periódicos, simular movimentos suaves e são a base de grande parte dos cálculos relacionados ao trabalho com visualizações bidimensionais.
[7] Aproximadamente traduzido para o título desta seção.
[8] Provavelmente, porém não provado. A natureza raramente é uma ciência exata e muito menos escrita em fórmulas explícitas disponíveis para consulta. O que existe, de fato, são hipóteses que revelam que quando certas estruturas matemáticas são usadas, vantagens evolutivas seriam asseguradas.
[9] Tucker, V. A. et al (2000). Curved flight paths and sideways vision in peregrine falcons (Falco peregrinus). The Journal of Experimental Biology 203(24): pags.3755-3763.
[10] Ridley, J. N. (1982). Packing efficiency in sunflower heads. Mathematical Biosciences 58(1): pags.129-139.
[11] No capítulo 3 é equivalente a questão do o que parametrizar.